Terebess
Ázsia E-Tár
«
katalógus
«
vissza a Terebess Online nyitólapjára
Szuan-pan,
a kínai golyós számológép
Elektronikus
kiadás: Terebess Ázsia E-tár
Kínai
számolás
> szórólap
Abakusz
> Terebess Ázsia Lexikon
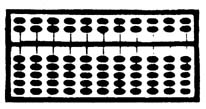
Áll
egy
fa keretből, fa gyöngyökből és sorokból. A keret két részre van osztva, a felsőre
és az alsóra.
A sorok száma mindig szükség szerint változik. A közönséges
szuan-pan 9, 11 vagy 13 soros.
2-2 gyöngy található az osztóléc felett, 5-5
az osztóléc alatt. Az osztóléc felettit "felső gyöngyöknek" és az osztóléc
alattit "alsó gyöngyöknek" nevezzük.
A legmagasabb gyöngyöket "legfelső
gyöngyöknek" nevezzük.

A gyöngyök értéke
Minden
felső gyöngy azonos ugyanazon sor 5 alsó gyöngyével.
Minden alsó gyöngy azonos
a rákövetkező jobboldali sor 10 gyöngyével.
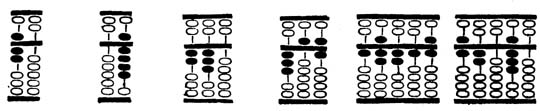
A következő ábrák az alábbi számokat
mutatják:
7, 9, 23, 356, 17.216 és 6.208
A
nullátt egy hézag jelzi. Nehézségek adódhatnak, ha ezt nem követi számjegy. Így
a 2. ábra jelenthet 7, 70, 700, 7.000, 70.000 vagy 0,7, 0.007 stb. értéket. Ügyelni
kell a helyértékekre, amit a használó maga szab meg.
Van egy szabály, ami
kimondja, hogy a számolási eljárás alatt az alsó gyöngyök legalsóját valamint
a felső gyöngyök legfelsőjét, amennyire lehet, keveset használják, mivel az 5-ös
számot egy felső gyöngy ábrázolja és a 10-es számjegyet a következő sor alsó gyöngye.
Az ujjak használata
A szuan-pannal történő számoláskor csak 3 ujj használata szükséges. A hüvelykujj mozgatja az a1só gyöngyöket felfelé, a mutatóujj a felső gyöngyöket lefelé és a középső ujj a felső gyöngyöket felfelé és lefelé is. A fennmaradt két ujjat vagy tegyük keresztbe vagy mutassunk velük felfelé, hogy elkerüljük a gyöngyök érintését. Ez rendkívül fontos, hogy a pontosságot biztosítsuk. Egy balkezes használhatja a balkezét. Szükségtelen mondani, hogy a mozgásirány - jobbra vagy balra - megfordul és hogy a gyöngyök értéke szintén megfordul, ammenyiben ez a sorokra vonatkozik.
Összeadás
Bizonyos
fokig mindenki tud a szuan-pannal összeadni, anélkül, hogy tanították volna. Vegyük
pl. a következőt:
Hogyan végezné el a "5+3" műveletet?
A 8.
és a 9. ábra mutatja a helyes eljárást, amihez további magyarázat nem szükséges.

A szükséges szabályok
Néhány
szabály szükséges. Pl: "7+8". Egy felső gyöngyöt lefelé és két alsó
gyöngyöt felfelé mozgat, hogy 7-t ábrázoljon.
Annak megállapításakor, hogy
nincs mód arra, hogy ehhez a sorhoz 8-t hozzáadjon, egészen világos, hogy a rákövetkező
sor alsó gyöngyét felfelé kell mozgatni, és azután két gyöngyöt azon a soron,
amelyik a 7-t ábrázolja, kivonni. A 10. ábra szerint (7-es szám) és a 11. ábra
(15-ös szám) szerint csak két mozdulat szükséges; egy alsó gyöngy eltolása felfelé
a következő soron, ami ez esetben 10-et tesz ki, és két alsó gyöngy eltolása lefelé
az értéksoron, ami 7-et tesz ki. Az a gyakorlat, hogy legelőször az egyik gyöngyöt
az értéksorban lefelé tolni, és azután az egyik gyöngyöt a következő sorban felfelé.
A szabály tehát mint ez esetben 8-t hozzáadni, a következő:
"8, 2-t
elmozdítani, 1-t előremenni".

Hasonló
módon mutatja a 12. ábra és 13. ábra a "13+9" művelet elvégzését:
"9, 1-t elmozdítani, 1-t előremenni".

Az összeadáara vonatkozó szabályok
Tanulja
meg kívülről a szabályokat:
1. 1 (ahol több mint 4 van) 5-t lefelé tolni,
4-t elmozdítani
2. 2 (ahol több mint 2, azonban kevesebb mint 5 van) 5-t
lefelé tolni, 3-t elmozdítani
3. 3 (ahol több mint 2 van) 5-t letolni, 2-t
elmozdítani
4. 4 (ahol több mint 1 van) 5-t letolni, 1-t elmozdítani
5. 6 (ahol több mint 5, azonban kevesebb mint 9 van) 1-t hozzáadni, 5-t elmozdítani,
1-t előremenni
6. 7 (ahol 5, 6 vagy 7 van) 2-t hozzáadni, 5-t elmozdítani,
1-t előremenni
7. 8 (ahol 5 vagy 6 van) 3-t hozzáadni, 5-t elmozdítani, 1-t
előremenni
8. 9 (ahol 5 van) 4-t hozzáadni, 5-t elmozdítani, 1-t előremenni
9. 1 (ahol 9 van) 9-t elmozdítani, 1-t előremenni, azaz 1-t a rákövetkező baloldali
soron hozzáadni
10. 2 (ahol 8 vagy 9 van) 6-t elmozdítani, 1-t előremenni
11. 3 (ahol több mint 7 van) 7-t elmozdítani, 1-t előremenni
12. 4 (ahol
több mint 6 van) 6-t elmozdítani, 1-t előremenni
13. 5 (ahol több mint 7
van) 5-t elmozdítani, 1-t előremenni
14. 6 (ahol 4 vagy 9 van) 4-t elmozdítani,
1-t előremenni
15. 7 (ahol 3, 6 vagy 9 van) 3-t elmozdítani, 1-t előremenni
16. 8 (ahol 2, 3, 4, 7, 8 vagy 9 van) 2-t elmozdítani, 1-t előremenni
17.
9 (ahol több mint 1 van) 1-t elmozdítani, 1-t előremenni
Ezek a szabályok
maguktól értetődnek. A gyakorlatban mindenki tud hasonló szabályokat kiokoskodni,
amennyiben a matematikát segítségül veszi.
Gyakorlatba átültetett szabályok
Nézzük
meg, hogyan jutunk el a suan-panban az eredményhez több összeadandó esetén a fenti
szabályok segítségével.
50.007 + 5.005 + 804 + 100.005 = 155.821
A 14.
ábra mutatja az első összeadás eredményét és a 15. ábra az utolsóét. Próbálja
meg és ellenőrizze, hogy az Ön eredménye megegyezik-e a fentivel. Ahol nem szükséges
szabály, ott nincs semmi említve. Az alkalmazott szabályok 13. sz, 4. sz, 13.sz

Kivonás
Bizonyos
fokig ön használni tudja a szuan-pant erre a célra, pontosan ahogy ezt az összeadásnál
tette.
Vegyük pl. a "9-4" műveletet. A 16. ábra és 17. ábra világossá
teszi, hogy még egy pillanatig sem kell gondolkodnia, hogy az eredményt megkapja.
Amennyiben 4-t elmozdít, megvan az eredmény.

A következő egy olyan eset, ahol szükséges egy bizonyos szabály alkalmazása.
76 - 4 = ?
Amennyiben a "4. - 1-t hozzáadni, 5-t elmozdítani" szabályt alkalmazza a kisebbítendőnél - 18 ábra - megkapja az eredményt, 72-t, amint azt a 19. ábra mutatja.

A szabályok
Azok
akik az összeadás szabályaival megismerkedtek, maguk is könnyen össze tudják állítani
a kivonásra vonatkozó szabályokat. Állítsa fel a szabályokat és egyeztesse a következőkkel
és tanulja meg kívülről;
1. 1 (ahol 5 van) 4-6 hozzáadni, 5-t elmozdítani
2. 2 (ahol 5 vagy 6 van) 3-t hozzáadni, 5-t elmozdítani
3. 3 (ahol 5, 6 vagy
7 van) 2-t hozzáadni, 5-t elmozdítani
4. 4 (ahol 5, 6, 7 vagy 9 van) 1-t hozzáadni,
5-t elmozdítani 5. 1 (ahol nulla vagy van) 10-t elvenni azaz 1 gyöngyöt a következő
baloldali soron elmozdítani, 9-t hozzáadni
6. 2 (ahol nulla vagy 1 van) 10-t
elvenni, 8-t hozzáadni
7. 3 (ahol nulla, 1 vagy 2 van) 10-t elvenni, 7-t hozzáadni
9. 4 (ahol nulla, 1, 2 vagy 3 van) 10-t elvenni, 6-t hozzáadni 5. 5 (ahol nulla,
1, 2, 3, vagy 4 van) 10-t elvenni, 5-t hozzáadni
10. 6 (ahol nulla, 1>
2, 3, 4 vagy 5 van) 10-t elvenni, 4-t hozzáadni
11. 7 (ahol nulla, 1, 2, 3,
4, 5 vagy 6 van) 10-t elvenni 3-t hozzáadni
12. 8 (ahol nulla vagy bármilyen
más 8 alatti szám van) 10-L elvenni, 2-t hozzáadni
13. 9 (ahol nulla vagy
bármilyen más 9 alatti szám van) 10-t elvenni, 1-t hozzáadni
Szükségtelen hozzáfűzni, hogy az összeadás szabályait a kivonásnál is alkalmazza,
ott, ahol az összeadást a fenti szabályokban alkalmaznia kell.
Példák
Vonja ki a 9, 4, 7 és 3 számot a 215-ből. Állítsa be a szuan-panonon a 215-ös számot. Alkalmazza az 5. sz és 4. sz szabályt, erre megkapja a 20. ábrán látható eredményt, azután a 11. sz-t (mivel a tízesekben nulla van, mozdítsa el a százasok egyikét, és adjon hozzá 9-t tizesekben) és utána a 3.sz-t. Az eredményt a 21. ábrán látható.

Vonja
ki a 340, 14.918, 9.008 és 2.007 számot a 28.547-ből. Állítsa be a szuan-panon
a 29.547-es számot. Alkalmazza a 3. sz-t és mozdítson el 4-t. Azután mozdítson
el 10.000-t, alkalmazza a 9. sz, 13. sz, 5. sz, 6. sz, (a maradékot a 22. ábra
mutatja) 13. sz és 11. sz szabályokat.
Az eredmény a 23. ábrán látható.
Ha a szuan-pan segítségévei összeadni és kivonni tudunk, lehetőség van az eljárás
eredményeit ellenőrizni, amennyiben a kivonás helyett összeadást használunk és
fordítva.

Szorzás
Ugyanaz
a szorzótábla, mint amit a matematikában is használunk, megtalálható a szuan-pan
alkalmazásánál is.
2 x 8 = 16 vagy 3 x 8 = 24 mindkettőre vonatkozik. A kérdés
csak az, hogy a szuan-pannal hogy megy végbe.
A szabály azt mondja, hogy akár
a szorzó akár a szorzandó lesz mozgásban, és amint mozgásban van, az egyesek sora
a tízesek sora lesz. Ezáltal a "6 x 2" feladatnál először a 6-t ábrázoljuk.
Gondolatban mondja magában, hogy 2 x 6 = 12 és mozdítsa el a felső gyöngyöt (5)
és vegyen 2 gyöngyöt a rákövetkező soron úgy, hogy az egykori egyesek sora, azaz
ahol a 6-os volt jelölve, a tízesek sora legyen.

Néhány példa elegendő az egyszerű szorzások megértéséhez.
Egy számjegyű szorzó
Vegyük
a következő példát:
4.638 x 7=?
A
következő négy ábra szemlélteti a megoldást.
Először a szuan-pan bal oldalán
állítsa be a 4.638-as számot és a 7-t a jobb oldalon. Kezdje azzal, hogy a szorzandó
utolsó számjegyét 7-tel megszorozza, változtassa azt 5-re és adjon hozzá 6-t a
következő azaz a csatlakozó jobb soron. Ekkor a szuan-pan a 26. ábrán láthatót
mutatja.

Utána
szorozza a szorzandó utolsó előtti 3-as számjegyét 7-tel. Mozdítson el 1-t és
adjon 1-t hozzá a következő soron. Ellenőrizze, hogy az öné a 27. ábra eredményével
megegyezik-e.
Utána a szorzandó hátulról a harmadik számát, 6-ot szorozza
7-tel. Adjon hozzá három alsó gyöngyöt, mozdítson el egy felső gyöngyöt és adjon
hozzá két gyöngyöt a következő soron. Hasonlítsa össze a 28. ábrán lévő eredménnyel.

Végül szorozza az első 4-es számot 7-tel. Ismeretes, hogy a szorzat 28. Mozdítson el két alsó gyöngyöt és adjon hozzá 8-t a következő soron. Mivel ott "4" van, alkalmazza a 8. sz-t - "2-t elmozdítani, 1-t előremenni" - Hasonlítsa össze a kapott eredményt a 29. ábrával.
Ugye nem szükséges említeni, hogy képtelen szorzási műveletet elvégezni az, akinek az összeadásban nincs alapos gyakorlata.
Több számjegyű szorzó
Ha
a szorzóban több mint egy számjegy található, akkor azt mondja a szabály, hogy
azzal a számjeggyel kell kezdeni, amelyik a szorzóban balról az első és a szorzandóban
a jobb oldalon a második.
Jelen feladatnál : 963 x 148 =
szorzó szorzandó
3 x 4
3 x 8
3 x 1
Az
eredmény a 30. ábrán látható.
Az első szorzási lépés eredménye 444. Ügyeljen
arra, hogy a 3-as szám a szorzáskor - "3 x 4" - érintetlen maradjon.
A szorzat egyes helyiértékü számait a szorzandóból kiindulva a második sorra tesszük
és ez lesz 3.144. Végül a 3-t szorozzuk 1-gyel. Mozdítson el hármat és adjon hozzá
3-t a következő soron, ami 444-et tesz ki, mint ahogy a 30. ábra mutatja.
Azután lesz a 6 mégegyszer 4-, 8-, és 1-gyel szorozva. Az eredmény leolvasható
a 31. ábráról.
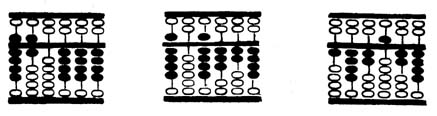
Ugyanezen a módon szorozzuk meg a 9-t ezzel a három számmal és megkapjuk az eredményt; 142.524, mint ahogy a 32. ábrán látható. Magától érthetődik, hogy sok összeadási szabályt kell alkalmazni, hogy a szorzásokat elvégezhessük.
Hogy világosabbá tegyük, hogy a számok milyen sokasága használatos a szorzáskor, minimum néhány példa bemutatása szükséges.
Milyen lépésekre van szűkség ahhoz, hogy e 2.435 x 1.875 szorzási művelet eredményeként szorzatkért a 4.565.625 számot megkapjuk?
A
33. ábra mutatja a gyöngyök első mozgatásából adódó eredményt,
(5 x 8, 7,
5, 1 = 1.875) a 34. ábra a másodikból adódót (3 x 8, 7, 5, 1), a 35. ábra a harmadikból
adódót (4 x 8, 7, 5, 1) és a 36. ábra az utolsó mozgás eredményét (2 x 8, 7, 5,
1).


Hasonlítsa össze a 37 - 41.-ig menő ábrákat a mozgásokkal, amelyek révén megkapjuk a "26.739 x 16.482" szorzási feladat eredményét, a szorzatot "440.712.198" összeget.
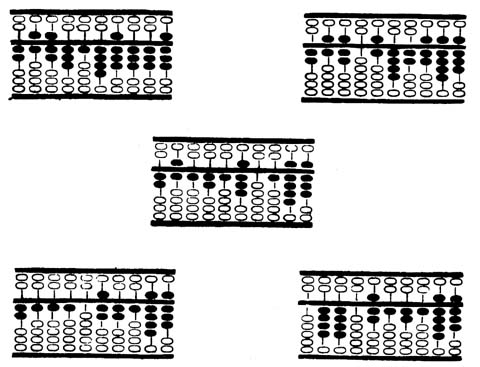
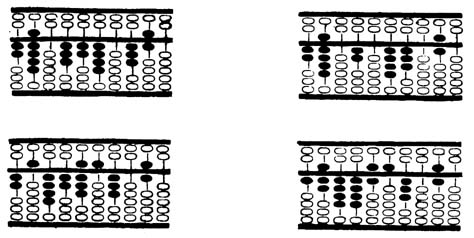
A következő példa: 29.034 x 6.009 = 174.465.306
A 42 - 45. ábrák mutatják az eljárást, ahogy az eredményt megkapjuk.
Óvatosság ajánlatos annál a sornál. ahol összeadásra kerül sor. Az egyeseket és a tízeseket meg kell különböztetni.
Nehézségek adódhatnak olyan számok szorzásakor mint 998 x 89. Ha megállapítjuk, hogy számításainkhoz nem áll elegendő gyöngy rendelkezésre, akkor ilyen esetekben a felső gyöngyöt 5. helyett 10-ként kezelhetjük és az alsó gyöngyöt olyan gyakran használhatjuk, amilyen gyakran csak szükséges.
Osztás
Mig a szorzásban csak kevés szabály szükséges, addig az osztáskor számos szabály szükséges, melyeket a tanuló maga is összeállíthat.
A sorok értéke
Az osztásban a rögzített sorok értéke, ellentétben a szorzással, megváltozik. Az egyesek tízesekre változnak. Ha pl. azt a szabályt alkalmazzuk, hogy "1 osztva 2 = 0.5" (az egyszerűség kedvéért mondhatunk 5-t), akkor 0.5 kerül ábrázolásra úgy, hogy azt követően 4-t pontosan azon soron, amelyiken az 1-es található hozzáadunk. (Hozzon egy felső gyöngyöt le és mozdítson egy alsót el.) Ez a szorzásnak a fordított menete, ahol az egyesek tízesekké válnak.
Természetesen világos, hogy mindenkinek jártasnak kell lennie az összeadási, kivonási és szorzási műveletekben mielőtt az osztással probálkozna.
Ha
egy számot 1-gyel osztunk, akkor nem kell semmilyen szabályt figyelembe venni.
Ha azonban egy szuan-pant használunk, akkor a számjegyeket az eredeti sorukból
a következő bal sorra kell átvinni. Ennek okát a 2. bekezdésben ma-gyarázzuk meg.
Ha pl. 234-et osztunk 1-gyel, először a 2-t el kell mozdítani úgy, hogy azt követően
két gyöngyöt a következő sorra átviszünk és pontosan így járunk el a 3-as és 4-es
szám esetén. Eredményként a 3 azon a soron lesz található, amelyiken eredetileg
2 volt és 4 azon a soron, amelyiken 3 volt.
A soroknak a változtatása azon
okból szükséges, hogy csak így marad a többi szám a következő számolási műveletekre
érintetlen.
A szabályok
Osztás kettővel:
1.
1 osztva 2-vel = 5. (Ez fent magyarázásra került. 1, 10 vagy 1.000 osztva 20-szal
vagy 0.2 vagy 2.000-rel ugyanaz az eset.)
2. Ahol 2 vagy 3 van, 2-t elmozdítani,
1-t előremenni.
3. Ahol 4 vagy 5 van, 4-t elmozdítani, 2-t előremenni.
4. Ahol 6 vagy 7 van, 6-t elmozdítani, 3-t előremenni.
5. Ahol 8 vagy 9 van,
8-t elmozdítani, 4-t előremenni.
Osztás hárommal:
1.
1 osztva 3-mal = 3 (azaz úgy, hogy azt követően az egyhez két gyöngyöt hozzászámolunk)
plusz 1, a maradék /úgy, hogy 1 gyöngyöt a legközelebbi jobb sorra átviszünk.
(Ügyeljen arra, hogy ezt vagy bármelyik maradékot 3-mal vagy egy másik számmal
ismét osztani kell, aszerint ahogy alakulnak)
2. 2 osztva 3-mal = 6 plusz
2 (l. az előző szabályt)
3. Ahol 3, 4 vagy 5 van, 3-t elmozdítani, 1-t előremenni
(amennyiben 4 a maradék; miután 3-t elmozdítottunk, 1 megmarad. Ha szükséges,
osszunk 3-mal. Ugyanezt a szabályt alkalmazza a többi maradéknál is.)
4. Ahol
6, 7 vagy 8 van, 6-t elmozdítani, 2-t előremenni.5. Ahol 9 van, 9-t elmozdítani,
3-t előremenni.
Osztás néggyel:
1.
1 osztva 4-gyel = 2 plusz 2
2. 2 osztva 4-gyel = 5
3. 3 osztva 4-gyel
= 7 plusz 2
4. Ahol 4, 5, 6 vagy 7 van, 4-t elmozdítani, 1-t előremenni
5. Ahol 8 vagy 9 van, 8-t elmozdítani, 2-t előremenni.
Osztás öttel
1.
1 osztva 5-tel = 2
2. 2 osztva 5-tel = 4
3. 3 osztva 5-tel = 6
4.
4 osztva 5-tel = 8
5. Ahol 5, 6, 7, 8 vagy 9 van, 5-t elmozdítani, 1-t előremenni.
Osztás hattal:
1.
1 osztva 6-tal = 1 (a gyöngyök mozgatása nem szükséges) plusz 4
2. 2 osztva
6-tal = 3 plusz 2
3. 3 osztva 6-tal = 5
4. 4 osztva 6-tal = 6 plusz 4
5. 5 osztva 6-tal = 8 plusz 2
6. Ahol 6, 7, 8 vagy 9 van, 6-t elmozdítani,
1-t előremenni.
Osztás héttel:
1.
1 osztva 7-tel = 1 plusz 3
2. 2 osztva 7-tel = 2 plusz 6
3. 3 osztva
7-tel = 4 plusz 2
4. 4 osztva 7-tel = 5 plusz 5
5. 5 osztva 7-tel = 7
plusz 1
6. 6 osztva 7-tel = 8 plusz 4
7. Ahol 7, 8 vagy 9 van, 7-t elmozdítani,
1-t előremenni.
Osztás nyolccal:
1.
1 osztva 8-cal = 1 plusz 2
2. 2 osztva 8-cal = 2 plusz 4
3. 3 osztva
8-cal = 3 plusz 6
4. 4 osztva 8-cal = 5
5. 5 osztva 8-cal = 6 plusz 2
6. 6 osztva 8-cal = 7 plusz 4
7. 7 osztva 8-cal = 8 plusz 6
8. Ahol
8 vagy 9 van, 8-t elmozdítani, 1-t előremenni.
Osztás kilenccel:
1.
1 osztva 9-cel = 1 plusz 1
2. 2 osztva 9-cel = 2 plusz 2
stb.
Osztás egy számjeggyel
Állapítsuk meg, hogyan kell ezekkel a szabályokkal dolgozni. A következő 46. és 47. ábra a 123456789 számot ábrázolják, amelyet 2-vel osztottak és az eredményt.

Az alkalmazott szabályok; 1, 2, 2. 1, 3, 3, 1, 4, 4, 1, 5, 5, 1. Ügyeljen a maradékokra.
Ellenőrizze a műveleteket a szuan-panon. Hasznosítsa számolási ismereteit és gyakoroljon,
amennyit csak tud.
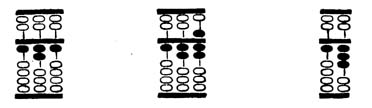
Segítségül az alábbi gyakorlatok hasznosak lesznek. A
48., 49. és 50. ábra bemutatja a "91 osztva 7 = 13" műveletet. Először
a szuan-panon beállítjuk a 91-es számot. Az alkalmazott szabályok;7 (l. 48. ábra),
2 (l. 49. ábra) és 7. (l. 50. ábra).
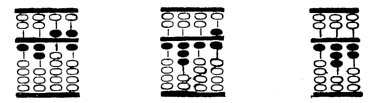
Az
51., 52., 53. ábra egy következő feladatot. mutatnak be.
1.056 osztva 8 =
132. Az alkalmazott szabályok: 1 (l. 51. ábra), 2., 8. (l. 52. ábra) és 1., 8.
(l. 53. ábra).
Az osztó nagyobb mint 10:
Ha
az osztó nagyobb mint 10, akkor úgy a szorzást mint az osztást is kiegészítően
alkalmazni kell. Az osztást kezdjük először a tízesekkel, ha az osztó egy kétszámjegyű
szám, és a százasokkal, ha az osztó egy háromjegyű szám. Vegyük a következő példát:
Osszunk el 245,- €-t 25 ember között egyenlően.
Állítsa be a szuan-panon a
245,- €-t. Egy pillanat alatt felismeri, hogy 245 kevesebb mint 25 x 10. Ha azt
a szabályt alkalmazza, hogy "2-t elmozdítani, 1-t előremenni", azaz
20 ember kap 10-10,- €-t. A maradék 45,- € nem elég, hogy a többi 5 ember 10-10
€-t kapjon.
Ahhoz, hogy ezt a problémát megoldjuk, egy másik szabályra van szükség. Ez az, hogy "azt követően, hogy megállapítja, hogy 2 nem elég az osztáshoz" alakítsa át a 2-t 9-re, marad 2 (azaz adjon minden embernek - 10,- € helyett - 9,- €-t, 2,- € maradékkal. Nézze meg, hogy a maradék elég nagy-e, hogy a többi 5 embernek 9,- €-t adjon. A maradék 65,- €. Vonja ki a 45,- €-t, ami 9,- € x 5 szorzata, és ezzel az 5 ember mindegyike is 9,- €-t kap. A maradék 20,- €, ahogy ez 54. ábra látható. Ahhoz aztán, hogy ezt a maradék 20,- €-t 25 ember között elossza, meg kell ismételni az előbb említett szabályt úgy, hogy 2-ből 9+2-t csinál, azaz 20 ember mindegyikének ad 0,90 €-t, 2,- € maradékkal. Utána megállapítja, hogy a maradék nem elég arra, hogy a maradék 5 ember mindegyikének is 0,90 €-t adjon. 4,50 €-re van szüksége, hogy az 5 ember között ezt kiosszthassa, de a maradék csak 2,- €.
Egy további szabályt kell segítségül venni. Ez a szabály azt mondja, azt követően, hogy megállapítást nyert, hogy a maradék az osztásra nem elegendő, levonhat 1+2-t, azaz a 20 ember mindegyikétől elvesz 0,10 €-t (mindegyiknek van 0,80 €-ja, ezért vonjon ki 1-t, 2,- € maradékkal (ezért adjon hozzá 2-t).
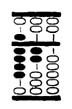
Ha feltételezi, hogy a hátralévő 5 ember mindegyike is kap 0,80 €-t, akkor 4,- €-re van szüksége, melyet egyenlően eloszt közöttük. Itt meg fogja állapítani, hogy egy további kivonással maradékként pontosan 4,- €-t kap. A hányados 9,80 € (hasonlitsa össze a 55. ábrával). Ismételje a műveletet, míg nem biztos benne. Egy ilyen kivonás mégegyszer megismételhető. Ha pl. egy számot 2-vel osztunk, vonjon le 2-t, marad 4, vagy 3-t, marad 6 stb. Ez a szabály más számokra is vonatkozik. Ha az osztó 8, vonjon ki 1-t marad 8, ha az osztó 9 vonjon le 1-t marad 9.
Ily módon az osztó egy tucat számig emelni lehet, amikor is azonban a módszer ugyanaz marad. Ha fentieket alaposan megértette, akkor könnyű lesz a többi osztási szabályt, ahol az osztó több mint 10 megértenie, vagy akár önállóan szabályokat felállítania.
Osztás 2-vel: (x...): megállapítva, hogy 2 nem elég az osztáshoz, alakítsa át a 2-t 9-re, marad 2. Újbból megállapítandó, hogy a maradék nem elegendő az osztáshoz, vonjon ki 1-t 9-ből, marad 2.
Osztás 3-mal: (x...): megállapítva, hogy 3 nem elegendő az osztáshoz,. alakítsa át a 3-t 9-re, marad 3. Újból megállapítva, hogy a maradék nem elegendő az osztáshoz, vonjon ki 1-t marad 3.
Osztás 4-gye1: - Osztás 7-tel: kihagyva.
Osztás 8-cal: (x...): megállapítva, hogy a 8 nem elegendő az osztáshoz, alakítsa át a 8-t 9-re, marad 8. Újból megállapítva, hogy a maradék nem elegendő az osztáshoz, vonjon ki 1-t marad 8.
Osztás 9-cel: (x...): megállapítva, hogy 9 nem elegendő az osztáshoz, tartsa meg a számot, marad 9. Újból megállapítva, hogy a maradék nem elegendő az osztáshoz, vonjon ki 1-t marad 9.
Egy további példa
Próbálja
meg a következő feladatot elvégezni: 9.147,60 € : 2.376 = ?
Á11ítsa be a 9.1476
számot a szuan-panon. /56. ábra/ Kezdje a 9-es számmal. Mozdítson el 6-t, menjen
előre 3-t. (Hányados első szemjegye) Vonja ki a 3 x 376 szorzatát (1.128) a maradékból,
31.476-ból. Először vonja ki a 3 x 3 (9) szorzatát a maradékból az alábbiak szerint:

3.147,60
- 900,00
__________
2.247,60 (maradék)
Aztán vonja ki a 3 x 7 (21) szorzatát a fenti maradékból:
2.247,60
- 210,00
__________
2.037,60 (maradék)
Végül vonja ki a 3 x 6 (18) szorzatát a maradékból:
2.037,60
- 18,00
__________
2.019,60 (maradék)
Hasonlítsa össze a 57. ábrával,
ahol a hányados 3.
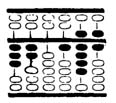
Azután ossza el a 20.196 maradékot 2.376-tal. Először váltsa át a 2-t 9-re, marad 2. A 2.196 maradék nem elegendő az osztáshoz. Vonjon ki 1-t 9-ből, marad 2. Akkor megvan a hányados második száma, 8 és 4.196 maradék. Vonja ki a 8 x 376 (3.008) szorzatát a maradékból. Először vonja ki a 8 x 3 (24) szorzatát a következők szerint:
419,60
- 240,00
_________
179,60 (maradék)
Aztán vonja ki a 8 x 7 (56) szorzatát a maradékból:
179,60
- 56,00
________
123,60 (maradék)
Végül
vonja ki a 8 x 6 (48) szorzatát a maradékból:
123,60
- 4,80
________
118,80 (maradék)
Hasonlítsa össze az 58. ábrával, ahol a hányados 38.
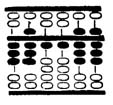
Végül ossza el a 1.188 maradékot 2.376-tal. Váltsa át az 1-t 5-re (a hányados utolsó számjegye), vonja ki a 5 x 376 (1.880) szorzatát a maradékból. Először vonja ki a 5 x 3 (15) szorzatát a maradékból:
18,80
- 15,00
________
3,80 (maradék)
Azután a 5 x 7 (35) szorzatát:
3,80
- 3,50
________
-,30 (maradék)
Végül az 5 x 6 szorzatát:
-,30
- -,30
_________
-,00
így nem marad maradék és a teljes
hányados 385. Hasonlítsa össze a 59. ábrával.